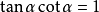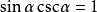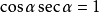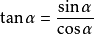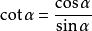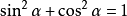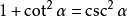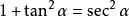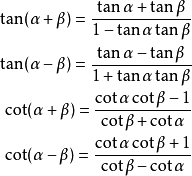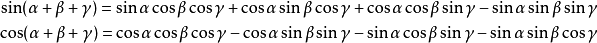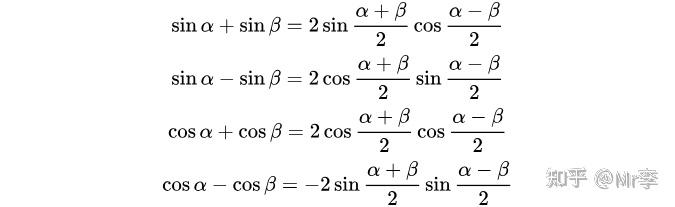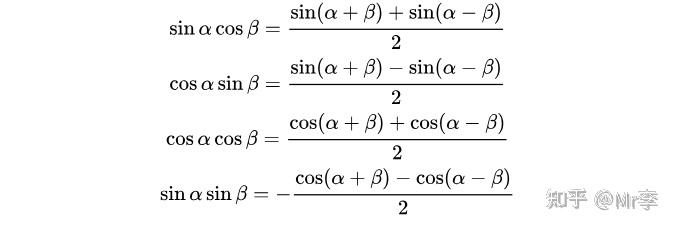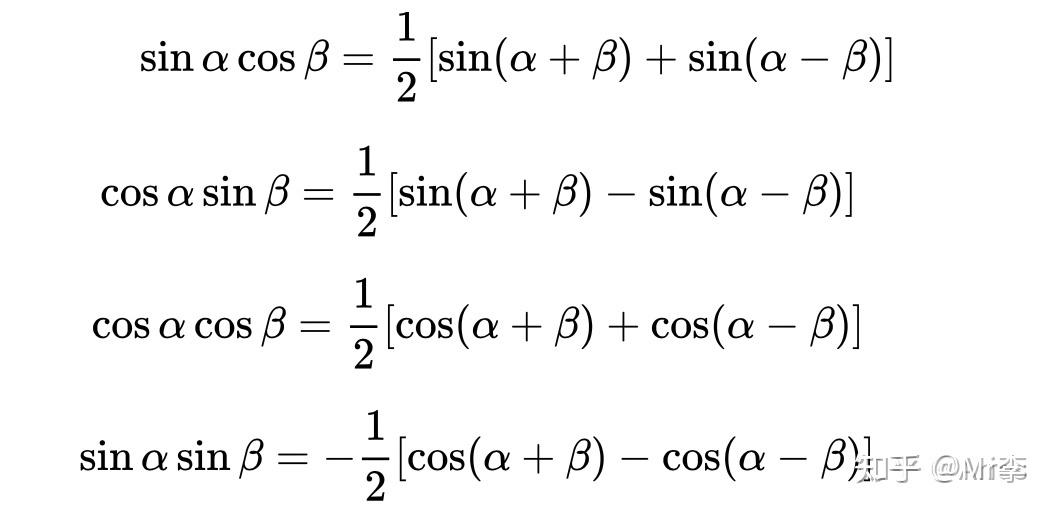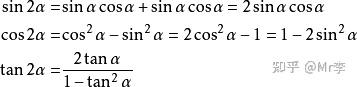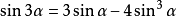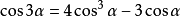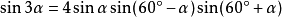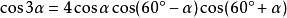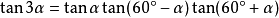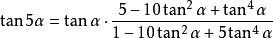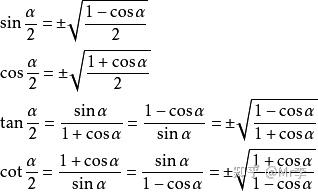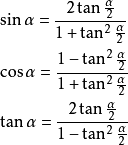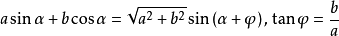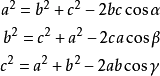三角函数公式汇总 + 记忆丨高中数学

温馨提示：内容较长，需耐心观看

三角函数公式包括和差角公式、和差化积公式、积化和差公式、倍角公式、诱导公式等。

本文重点：巧记和差化积、积化和差公式 （很多小伙伴记了就忘，忘了又记）

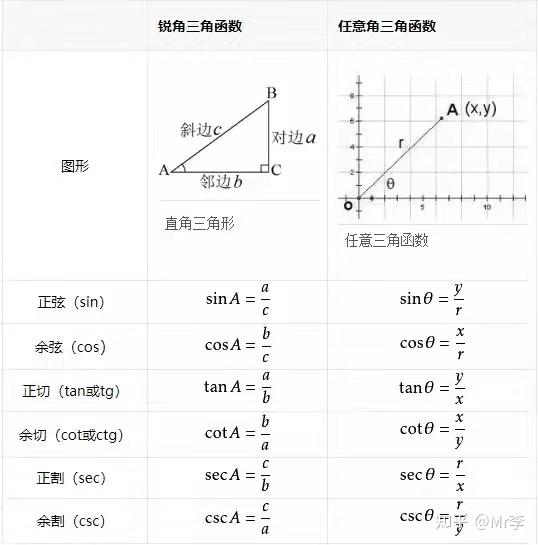
01 定义式

三角函数公式是数学中属于初等函数中的超越函数的一类函数公式。它们的本质是任意角的集合与一个比值的集合的变量之间的映射，通常的三角函数是在平面直角坐标系中定义的。

02 函数公式

倒数关系:

商数关系：

平方关系：

03 诱导公式

1. 公式 1：设α为任意角，终边相同的角的同一三角函数的值相等

$sin( 2kπ +α)=sinα(k∈Z)$

$cos(2kπ+α)=cosα(k∈Z)$

$tan(2kπ+α)=tanα(k∈Z)$

$cot(2kπ+α)=cotα(k∈Z)$

2. 公式二：设α为任意角，π+α的三角函数值与α的三角函数值之间的关系

sin(π+α) ＝－sinα

cos(π+α)＝－cosα

tan(π+α)＝ tanα

cot(π+α)＝cotα

3. 公式三：任意角α与 -α的三角函数值之间的关系

sin(－α)=－sinα

cos(－α)=cosα

tan(－α)=－tanα

cot(－α)=－cotα

4. 公式四：利用公式二和公式三可以得到π-α与α的三角函数值之间的关系

sin(π－α)=sinα

cos(π－α)=－cosα

tan(π－α)=－tanα

cot(π－α)=－cotα

5、公式五：利用公式一和公式三可以得到 2π-α与α的三角函数值之间的关系

sin(2π－α)=－sinα

cos(2π－α)=cosα

tan(2π－α)=－tanα

cot(2π－α)=－cotα

6、公式六：π/2±α与α的三角函数值之间的关系

sin(π/2+α)=cosα

sin(π/2－α)=cosα

cos(π/2+α)=－sinα

cos(π/2－α)=sinα

tan(π/2+α)=－cotα

tan(π/2－α)=cotα

cot(π/2+α)=－tanα

cot(π/2－α)=tanα

记背诀窍：奇变偶不变，符号看象限，即形如（2k+1）90°±α，则函数名称变为余名函数，正弦变余弦，余弦变正弦，正切变余切，余切变正切。形如 2k×90°±α，则函数名称不变。

04 基本公式：

4.1. 二角和差公式

口诀（正余弦两角和差公式）：

赛壳壳赛符号同，壳壳赛赛符号异。

1）正弦和差前后同号，余弦和差前后异号

2）正弦和差公式始终是 sin 与 cos 相乘; 余弦和差公式始终是 cos 与 cos 相乘，sin 与 sin 相乘

cos(α+β)=cosα·cosβ-sinα·sinβ

cos(α-β)=cosα·cosβ+sinα·sinβ

sin(α±β)=sinα·cosβ±cosα·sinβ

再说一下 tan 和差公式的记忆。

由下图可以看到，tan 和差公式的右边分式，分子与分母符号是不同的，而左边与分子符号又是相同的。这样我们就能通过左边确定等式右边的符号。

再记住上加下乘，就能把 tan 的每一项记住了。

4.2 三角和公式

注意！注意！注意！

人间大炮一级准备!!！

4.3 积化和差公式：

$${\displaystyle \sin \alpha \cos \beta ={\sin(\alpha +\beta )+\sin(\alpha -\beta ) \over 2}} \ {\displaystyle \cos \alpha \sin \beta ={\sin(\alpha +\beta )-\sin(\alpha -\beta ) \over 2}} \ {\displaystyle \cos \alpha \cos \beta ={\cos(\alpha +\beta )+\cos(\alpha -\beta ) \over 2}} \ {\displaystyle \sin \alpha \sin \beta =-{\cos(\alpha +\beta )-\cos(\alpha -\beta ) \over 2}} \$$

4.3.1 口诀法：

正余余正，正加正减；

余余正正，余加负余减。

d. 和差化积公式：

正加正，正在前；

正减正，余在前；

余加余，余并肩；

余减余，负正弦。

“两个口诀互逆，但推荐分别记忆，这样用起来会非常快！！

敲黑板，下面重点。

人间大炮二级准备!!!

前后项数统一：

积是一项，化和差后要 $\div2$ ；
和差是两项，化积后要成 $\times 2$ 。

内外项数统一：

括号内变量都是先 $\alpha + \beta$ ，再 $\alpha - \beta$ 。
化和差后是两项， $\alpha \pm \beta$ 两项不变；
化积后是一项， $\alpha \pm \beta$ 要 $\div2$ 变一项。

4.3.2 帅哥记忆法：

积化和差只需反过来说，即：

帅哥 = 帅 + 帅
哥帅 = 帅 - 帅
哥哥 = 哥 + 哥
负嫂嫂 = 哥 - 哥

本人更喜欢第一种方法，直接记忆好记并且快。

4.4. 倍角公式：

◆ 二倍角公式

推论：升幂缩角公式

降幂扩角公式

运用二倍角公式就是升幂，将公式 Cos2α变形后可得到降幂公式。

◆ 三倍角公式

◆ 四倍角公式

$sin4a=-4*[cosasina(2*sina^2-1)]$

$cos4a=1+(-8cosa^2+8cosa^4)$

$tan4a=(4tana-4tana^3)/(1-6*tana^2+tana^4)$

◆ 五倍角公式

◆ 半角公式

（正负由 $\alpha/2$ 所在的象限决定）

4.5. 万能公式

4.6 辅助角公式

4.7. 余弦定理

4.8. 三角函数公式算面积

定理：

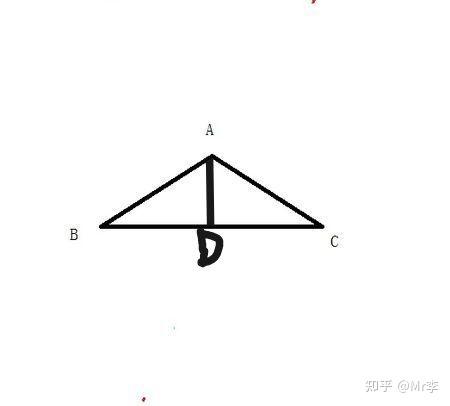
在△ABC 中，其面积就应该是底边对应的高的 1/2，不妨设 AD 边对应的高是 BC，那么△ABC 的面积就是 BCAD1/2。而 AD 是垂直于 BC 的，这样△ADC 就是直角三角形了，由此可以得出， $AD=$ $ACsinC$，将这个式子带回三角形的计算公式中就可以得到：S△ABC= $1/2absinC=1/2bcsinA=1/2acsinB$

同理，即可得出三角形的面积等于两邻边及其夹角正弦值的乘积的一半。

◆ 公式：

若△ABC 中角 A，B，C 所对的三边是 a,b,c：

则 S△ABC= $1/2absinC=1/2bcsinA=1/2acsinB$