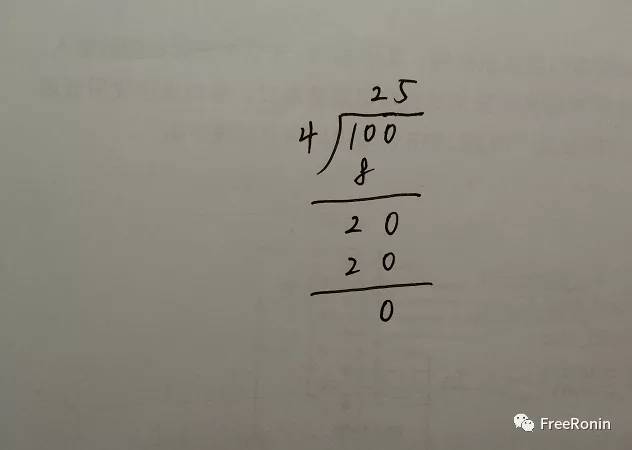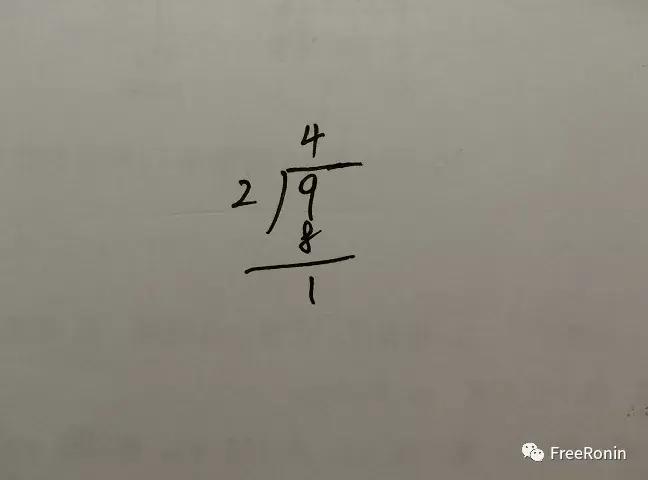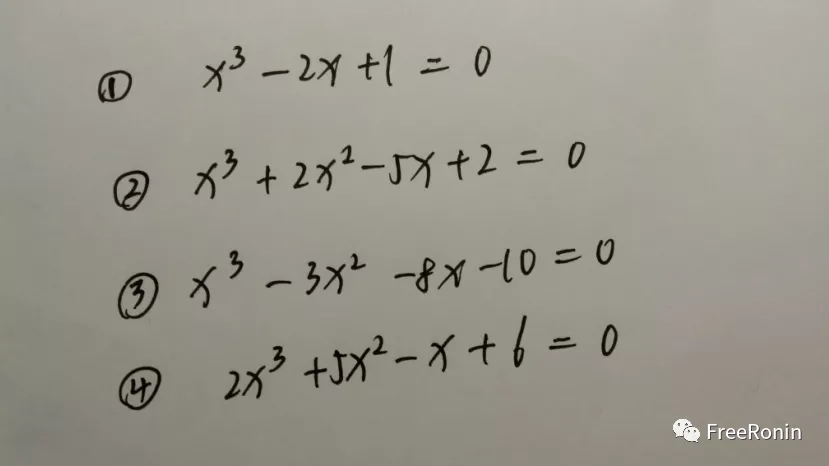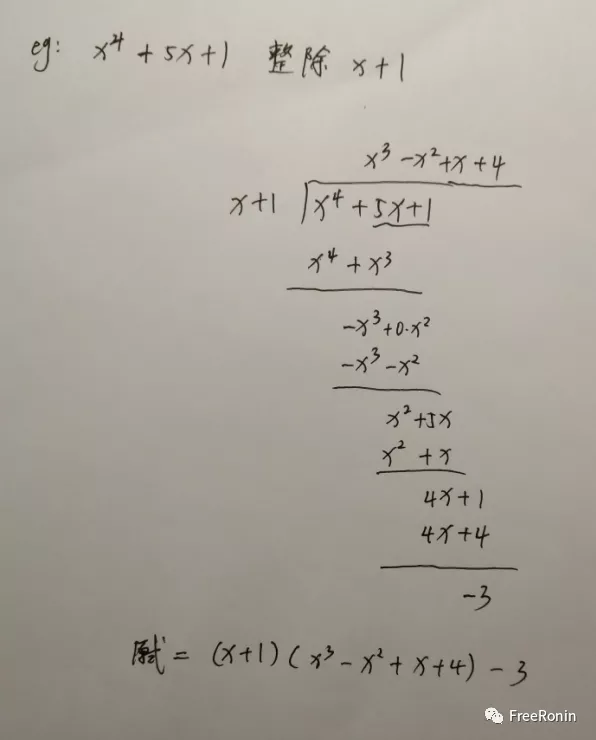首先，我们先介绍一下什么是大除法，怎么用，怎么去理解？

什么是大除法？

大除法 - 百度百科

可能大家看得有点懵，给大家举个栗子，大家就明白了。

比如我们正常的一个除数除以被除数：比如 100 除以 4,9 除以 2 等。

我们知道 100÷4=25，写过程为：

余数为零，说明这个数能被另一个数整除，也就是 4 可以被 100 整除，那么就有：

100=4×25

余数不为零，说明这个数不能被另一个数整除，也就是 2 不可以被 9 整除，那么就有：

9=2×4+1

那么，推广到多项式呢？

所以就有了今天的内容：

如果常数 C 等于 0，那么 这个多项式能被另一个多项式整除。

先来举一两个简单的例子：

先看第一个例子：

再看第二个式子：

继续第三个式子：

继续第四个例子：

**立方和公式**大家可以自行按此推导，其实这些都是需要记住的，如果会推导的话，记都不用记。

继续第五个例子：

当然，我们可以将其推导到更高次项也是完全可以的，这里就不再继续书写了。相信看到这里的童鞋基本都可以看懂了。

下面回到我们的正题，使用大除法（长除法）求解一元三次方程，当然更高次也是适用的。

还是那句话，百闻不如一见，看书不如看实验！

就以这四个式子为大家做个示范吧：

先看第一个式子：

按照今天提到的方法解：（直接假定我们知道解，然后去找关联，当然解一定是常数的因数里面的一个，包含 1 以及它本身）。

如果有去了解过我以前写的内容的话，应该都会发现，根一定都是常数项的因数中的一个。如一式子中的 1 的因数有（-1,1），正数负数范围内都考虑。

继续看第二个例子：

继续看第三个例子：

最后看第四个例子：

看，是不是也非常的简单，当然如果你能直接看出来一个解的话，那就直接非常简单了。

最后再说明一点，这个使用条件也是不能去求解分式根，因为分解难度大，所以是分式根的话，推荐使用双十字法进行求解。

文章如下：

数学技巧 || 双十字法巧解一元三次方程

最后，我们把它推到高次项，也给大家举个栗子。

**如果大家对大除法用的比较熟的话，其实进行降幂排列属于多余的，**进行降幂的目的主要是防止运算遗漏导致出错而已。

好了，以上就是本次的分享了！希望大家用得熟练~~

大致就写这么多了，由于号主也是在工作中只能闲下来的时候才会写一下，所以做工就会相当的粗糙，这篇文章或者这个技巧我个人希望的是能让需要的人看到，让更多的人知道还有这个方法，希望能看到这篇文章或者学到这个技巧的人能够走的更远，号主就只能走到这了，也希望对这个有研究的可以继续研究下去，让跟多的人学到，更多的人看到~~~

本文章选自知乎专栏《数学技巧||一元三次方程求解，大除法解一元三次方程！》(查看原文)，若侵犯版权，请联系站长删除。